[渣翻] Nonlinear Dimensionality Reduction by Locally Linear Embedding

非线性降维的局部线性嵌入(LLE)法

原文链接 [click]

Abstract

科学的许多领域依赖于探索性数据分析和可视化. 分析大量多元数据的必要性提出了降维的基本问题: 如何发现高维数据的紧凑表示. 在这里, 我们介绍了局部线性嵌入(LLE)法, 一种无监督的, 通过计算高维输入的低维的, 邻域保持嵌入的学习算法. 与聚类方法的局部降维不同, LLE将输入映射到一个低维的的单一全球坐标系, 它的最优解, 不涉及局部最优. 通过利用线性重建的局部对称性, LLE能够学习非线性流形的全局结构, 例如通过面或文本文件的图像生成的那些的全局结构.

Main Body

怎样判断相似? 我们对世界的感性认知通过处理大量的感觉输入得到, 例如包括形成图像的像素强度, 声音的功率谱, 以及铰接机构的关节角度. 虽然这种形式的复杂的刺激可以通过在高维矢量空间中的点来表示, 它们通常具有一个更加紧凑的描述. 现实世界中的一致结构导致了输入之间强的相关性(如图像中的相邻像素之间), 产生了在位于或接近一个平滑的低维流形的观测结果. 为了比较和分类这样的观测结果, 实质上由于现实世界的原因, 关键在于对这些低维流形的非线性集合建模.

对探索性分析和多元数据可视化感兴趣的科学家面临类似的降维问题[1]. 该问题, 如图1所示. 涉及将高维输入映射到一个低维“表示”的, 具有很多不同的观察模式的空间中. 之前解决该问题的方案基于多维尺度(MDS)[2], 试图通过保持成对数据点的距离(或广义上的距离[3])来求解嵌入模式. 这种距离可以用直线距离来测量, 或者选用更复杂的MDS例如Isomap[4]方法, 选用局限于观察到的输入数据的流形上的最短路径. 在这里, 我们采取一种不同的方法, 被称为局部线性嵌入(LLE), 即消除了估算广泛分离的数据点之间的成对距离的需要. 不同于以往的方法, LLE可以从局部线性拟合得到全局非线性结构.

LLE算法, 如图2概括一样, 是基于简单的几何直觉. 假设数据由$N$个维数为$D$的实值向量$\vec{X_i}$, 每个数据都是从一些潜在的流形采样所得. 只要有足够的数据(假设该流形可以无限采样), 我们预计每个数据点与其近邻位于或接近于流形的局部线性流形. 我们用其近邻的数据重建所得的线性系数刻画这些流形的局部几何形状. 重建误差由损失函数定义

$$\epsilon(W) = \sum_i|\vec{X_i} - \sum_j W_ij \vec{X_j}|^2$$

即所有数据点与其重建点的距离的和. 权重$W_{ij}$表示第$j$个数据点对第$i$个重建流形的贡献. 为了计算权重$W_{ij}$, 同时最小化损失函数, 我们添加两个约束. 首先, 每个数据点$\vec{X_i}$只会由其近邻进行重建, 并且强制设置$W_{ij} = 0$, 如果$\vec{X_j}$不在$\vec{X_i}$的近邻当中[5]. 其次, 权重矩阵的每一行的和为$1$, 即$\sum_jW_{ij} = 1$. 受以上条件约束[6]的最优权值$W_{ij}$的解可以通过求解最小二乘问题[7]解决.

最小化损失函数的受约束的权值服从一个重要的对称性, 即任何特定的数据点和其近邻, 具有旋转, 重缩放, 平移不变性. 通过对称, 它遵循该重建权重刻画每组数据组(数据点与其近邻)的固有几何特性, 而不是依赖的参考的特定帧的属性[8]. 注意, 平移不变性具体为权重矩阵的行的和为$1$进行约束强制.

假设数据位于或近似位于一个光滑非线性低维流形上, 其维度$d \ll D$. 为了得到一个良好的近似, 那么存在一个线性映射, 包括平移, 旋转和重缩放, 将数据组高维的坐标映射到流形上的全局内坐标. 在设计上, 重建权重$W_{ij}$将固有的数据的几何性质恰恰反映为这些变换的不变性. 因此, 我们希望他们在原始数据的空间局部的几何形状的表征在局部的流形上同样有效. 特别的, 由第$i$个数据点在$D$维中的权重$W_{ij}$应当与$d$的嵌入流形的权重相同.

LLE构建了基于上述想法的保邻域映射. 在该算法的最后步骤中, 每个高维观察$\vec{Y_i}$映射到低维向量$\vec{Y_i}$表示在流形上全局内部坐标. 通过选择$d$维向量$\vec{Y_i}$, 以尽量减少嵌入损失函数

$$\Phi(Y) = \sum_i|\vec{Y_i} - \sum_j W_ij \vec{Y_j}|^2$$

该损失函数, 和前一个类似, 基于局部线性重构误差, 但在这里我们固定权重$W_{ij}$, 对$\vec{Y_i}$进行优化. 等式(2)中所定义的嵌入损失是一个关于$\vec{Y_i}$的二次型. 受到条件的限制, 为使得该问题适定, 可以通过求解一个稀疏的$N \times N$的矩阵特征值问题[9], 其底部$d$个非零特征向量提供了一个有序的中心在原点的正交坐标.

该算法的实现很简单. 在我们的实验中, 数据点通过他们的欧氏距离或正则化的内积所确定的k近邻来进行重建. 对于这种LLE的实现方式, 该算法只有唯一一个自由参数, 近邻的个数$k$. 一旦确定近邻, 那么最佳权重$W_{ij}$和向量$\vec{Y_i}$便可以通过线性代数中的标准方法计算得到. 该算法包含如图2所示的三个步骤, 并且通过式(1)与式(2)来确定重建结果的全局最小与嵌入损失.

除了图1的已知确定流形结构的例子[10]之外, 我们同样将LLE方法应用到了脸部图像[11]与词向量文档[12]当中. 脸部图像与词向量的嵌入结果如图3与图4所示. 注意到嵌入空间的坐标是与有意义的属性密切相关的, 比如人脸的姿势与表情, 以及词汇的语义关联.

许多流行的用于非线性降维的学习算法并不共享LLE的良好特性. 用于自编码神经网络的迭代爬坡方法[13, 14], 自组织映射[15], 以及隐变量模型[16]都不能同时保证全局最优以及收敛性. 他们也往往涉及更多的自由参数, 例如学习效率, 收敛标准, 架构规范. 最后, 区别于其他的非线性方法均依赖于确定性退火方案[17]以避免局部极小解, LLE的优化特别容易处理.

LLE很好地进行扩展固定流形的维数$d$, 而且并不需要嵌入空间的离散网格化. 当越来越多的维度被添加到嵌入空间时, 现有的流形不会改变, 从而使LLE不必重新运行以计算高维嵌入. 与一些方法, 如主曲线和表面[18]或可添加组分模型[19], LLE实际上并受到非常低维的流形的限制. 此外, $D$的固有值本身可以通过分析损失函数的倒数, 其中, 从嵌入向量$\vec{Y_i}$所得到的权重被应用到原数据点$\vec{X_i}$上.

Martinetz, Schulten[20]和Tenenbaum[4]说明, LLE阐述了流形学习的一般原则, 重叠的局部近邻的共同分析,可以提供关于全局集合性质的信息. LLE的很多优良特性传承于Tenenbaum的算法, Isomap. 该算法被成功的用于非线性降维的类似问题当中. Isomap嵌入通过计算数据的的最短路径估计测地距离的方法进行优化. 而LLE选择不同的方法, 分析局部的对称性, 线性系数, 以及重建误差, 而不是全局约束, 对偶点距离和应力函数. 它因此避免了需要解决的大的动态规划问题,而且他也倾向于堆积出非常稀疏的矩阵, 其结构可以用与节省时间与空间.

LLE可能在数据分析和统计学习等方法的组合中更为有用. 例如, 在观察空间与嵌入空间之间的参数图可以通过监督神经网络[21]进行学习, 其目标值通过LLE生成. LLE也可以推广到更困难的应用当中, 比如在不相交的数据流形的情况下, 或者更简单的, 比如在时间序列观察的情况下.

也许应用LLE到各种问题的巨大潜力超出这里讨论, 鉴于传统的方法, 如PCA和MDS的广泛的吸引力, 该算法应当找到在科学的许多领域的广泛的应用.

图 1

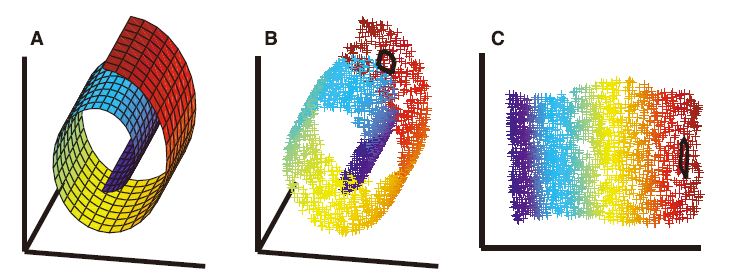
非线性降维问题, 如[10]所示的从三维数据(B)采样所得的二维流形(A). 无监督学习算法必须在没有明确地指明数据的嵌入方法的条件下, 发现流形上的全局内坐标. 图中的颜色说明了LLE所发现的保邻域映射; 而(B)和(C)的黑色轮廓线显示单个点的近邻. 与LLE不同的是, 通过主成分分析(PCA)[28]或者经典MDS将相对远的数据点映射到平面上的相对近的点的话, 将不能确定流形的底层结构. 注意局部降维的混合模型[29], 该问题利用数据聚类并且在每个数据簇上实施PCA解决, 并不涉及这里讨论的问题, 即如何将高维数据映射到低维的一个全局坐标系当中.

图 2

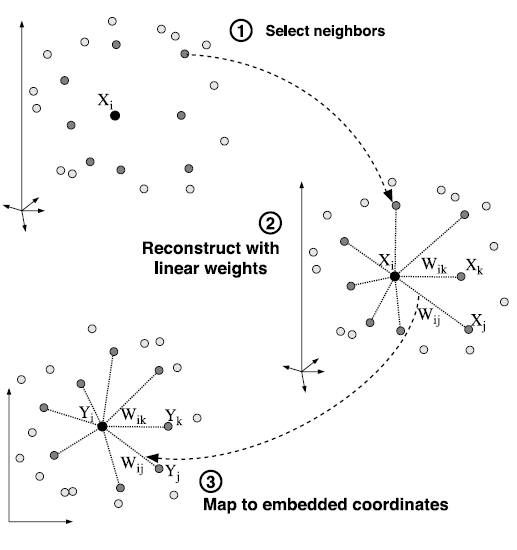
局部线性嵌入的步骤: (1) 指定每一个数据点$\vec{X_i}$的近邻(如通过选择每个数据点的k近邻); (2) 通过求解式(1)所示的最小二乘约束的问题, 计算通过线性重建的最优权重$W_{ij}$; 通过求解式(3)所示稀疏对称矩阵的最小特征值问题解决式(2)的最小值问题, 从而得到重建后最优的嵌入向量$\vec{Y_i}$. 尽管最佳权重$W_{ij}$和向量$\vec{Y_i}$易于通过线性代数的方法计算, 而数据点只能从近邻重建的约束可能会导致高维非线性的嵌入.

图 3

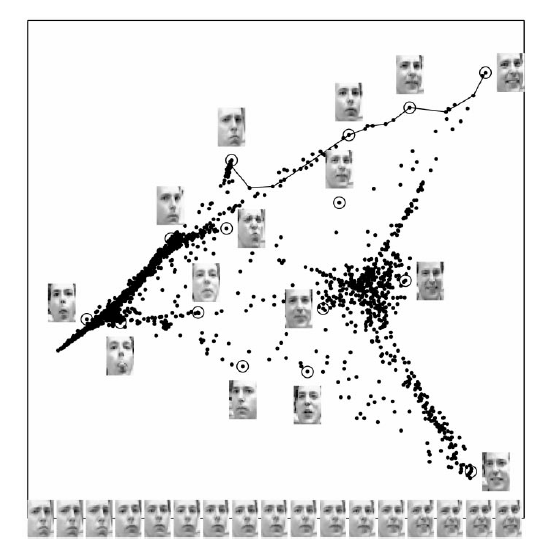
映射到嵌入空间中的脸部图像[11]可以通过LLE方法用前两个分量进行描述. 图中不同部分中的被圈中的点旁边的图像表示该点表示的图像. 底部的图像对应沿右上方路径(用实线连接的点)表示出了不同姿势和表情变化的一个具体的模式.

图 4

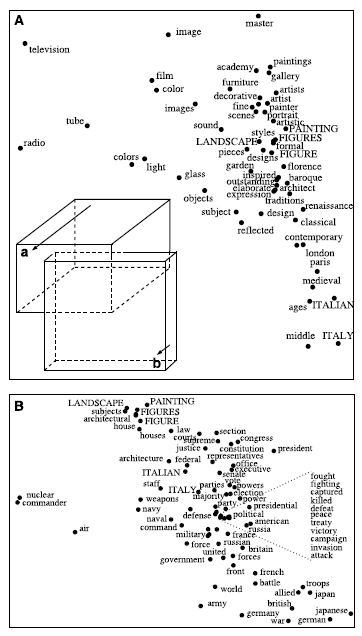
在连续语义空间安排单词的话, 每个单词都被初始化为不同语料库中出现频数的高维向量. 在每个文档词向量应用LLE方法, 得到每个单词的嵌入位置. 如图展示的有界区域(A)与(B)是利用LLE所得到的两个不同嵌入空间. 每个子图表示到LLE的第三和第四坐标的一个二维投影, 区域(A)(B)在这两个维度上高度重叠. (A)中的插图展示了到第三, 第四, 和第五坐标的一个三维投影, 从而展示出一个额外的维度, 使得在该维度上区域(A)(B)更易于被区分开. 图中在两个区域的交集的单词用大写表示. 注意到LLE将在连续语义空间中的单词用类似的上下文进行了连接.

References and Notes

1. M. L. Littman, D. F. Swayne, N. Dean, A. Buja, in Computing Science and Statistics: Proceedings of the 24th Symposium on the Interface, H. J. N. Newton, Ed. (Interface Foundation of North America, Fairfax Station, VA, 1992), pp. 208-217.
2. T. Cox, M. Cox, Multidimensional Scaling (Chapman & Hall, London, 1994).
3. Y. Takane, F. W. Young, Psychometrika 42, 7 (1977).
4. J. Tenenbaum, in Advances in Neural Information Processing 10, M. Jordan, M. Kearns, S. Solla, Eds. (MIT Press, Cambridge, MA, 1998), pp. 682-688.
5. 每个数据点的近邻集合可以通过多种方法进行遴选: 比如通过选择在欧几里得距离下的k个最近 邻, 或者可以通过考察固定半径的球中的所有数据点, 或者使用先验知识. 注意, 对于确定数 量的近邻, 通过LLE方法所确定的嵌入空间的维度应当严格小于近邻的数量.
6. 对于某些确定领域的应用, 人们也可能会限制其权重为正数, 因此要求每个数据点的重建结果必 须位于其近邻集的凸包内部.
7. 补充说明: 最优的通过每一个数据点的近邻所重建的结果的受约束权重可以通过封闭形式进行计 算. 考查一个特定的数据点$\vec{x}$及其近邻$\vec{\eta_j}$, 和归一化的重建权重$w_j$, 重 建损失$|\vec{x} - \sum_{j=1}^k {w_j\vec{\eta_j}}|$通过三个步骤来计算其最小值. 首先, 计算任意两个近邻的内积从而得到关联矩阵$C_{jk} = \vec{\eta_j} \cdot \vec{\eta_j}$, 以 及该关联矩阵的逆$C^{-1}$. 第二步, 计算拉格朗日乘数, $\lambda = \alpha / \beta$, 使得 其满足归一化的约束条件, 其中 $\alpha = 1 - \sum_{jk}{C^{-1}_{jk}(\vec{x} \cdot \vec{\eta_k})}$, $\beta = \sum_{jk}{C^{-1}_{jk}}$. 第三步, 计算重建权重, $w_j= \sum_{k}{C^{-1}_{jk}(\vec{x} \cdot \vec{\eta_k} + \lambda)}$. 如果关联矩阵$C$是 几乎奇异的, 那么可以(在求逆之前)加上一个小数乘上单位矩阵进行处理. 这相当于惩罚了在数 据采样过程中, 精确度在一定程度上相关性较大的权重.
8. LLE的确不需要在一个单一的坐标系统中描述的原始数据, 只要每一个数据点都相对的位于它的近 邻中.

9. 嵌入向量$\vec{Y_i}$利用确定的权值$W_{ij}$通过损失函数 $\Phi(Y) = \sum_i|\vec{Y_i} - \sum_j W_ij \vec{Y_j}|^2$确定. 通过这种约束 进行的优化使得问题可以良好地解决. 很显然, 向量$\vec{Y_i}$可以做平移变换而不影响 损失函数$\Phi(Y)$. 我们通过要求向量以坐标原点为中心, $\sum_i\vec{Y_i} = \vec{0}$, 来消除这个自由度. 另外, 为了避免退化的解决方案, 我们限制嵌入向量具有单位方差, 并且其 外积满足$\frac{1}{N} \sum_i{\vec{Y_i} \otimes \vec{Y_i}} = I$, 其中$I$表示一 个$d \times d$的单位矩阵. 那么现在损失函数可以定义为一个二次型, $\Phi(Y) = \sum_{ij}{M_{ij}(\vec{Y_i} \cdot \vec{Y_j})}$, 涉及到嵌入向量的内积以 及一个$N \times N$的对称矩阵

   $$M_{ij} = \delta_{ij} - W_{ij} - W_{ji} + \sum_k{W_{ki}W_{kj}}$$

   其中$\delta_{ij}$在$i = j$时取值为1, 否则为0. 直到嵌入空间的全局循环, 可以通过 计算底部的$d + 1$个特征向量求得最优嵌入[24]. 被我们忽视的矩阵底部的特征向量实际上 等价于单位向量, 表示一个特征值为$0$的自由变换. (忽略掉这些特征向量从而使嵌入满足 强制非零约束. )通过LLE方法在$d$维嵌入向量中找到剩下的$d$个特征向量. 注意到, 矩 阵$M$可以用稀疏矩阵$(I - W)^T(I - W)$进行储存和操作, 从而在$N$很大的时候提供 不错的计算效率. 而且, 其底部的$d + 1$个特征向量(对应于最小的$d + 1$个特征值) 可 以有效地计算得到, 而不是通过完全执行一次矩阵对角化[25].

10. 流形: 图1B($N = 2000$)中的数据点通过在如图1中的流形($D = 3$)上进行采样. k近邻 集($K = 20$)通过欧氏距离进行确定. 这个特殊的流形由Tenenbaum[4]引入. 他曾利用该流形 作为例子介绍Isomap方法可以学习他的整体结构.
11. 人脸图像: 同一张脸的多张照片($N = 2000$)被依次数字化为$20 \times 28$的灰度图 像. 在LLE中, 每一张图像被认为是一个$D = 560$的, 储存原始灰度的, 向量元素. k近邻 集($K = 12$)通过像素空间的欧氏距离进行确定.
12. 单词: 单词文档计数结果通过统计格罗里埃百科全书的$D = 31000$篇文章中的共 $N = 5000$个单词得到. k近邻集($K = 20$)通过统计向量的归一化内积进行确定.
13. D. DeMers, G. W. Cottrell, in Advances in Neural Information Processing Systems 5, D. Hanson, J. Cowan, L. Giles, Eds. (Kaufmann, San Mateo, CA, 1993), pp. 580-587.
14. M. Kramer, AIChE J. 37, 233 (1991).
15. T. Kohonen, Self-Organization and Associative Memory (Springer-Verlag, Berlin, 1988).
16. C. Bishop, M. Svensen, C. Williams, Neural Comput. 10, 215 (1998).
17. H. Klock, J. Buhmann, Pattern Recognition 33, 651 (1999).
18. T. J. Hastie, W. Stuetzle, J. Am. Stat. Assoc. 84, 502 (1989).
19. D. J. Donnell, A. Buja, W. Stuetzle, Ann. Stat. 22, 1635 (1994).
20. T. Martinetz, K. Schulten, Neural Networks 7, 507 (1994).
21. D. Beymer, T. Poggio, Science 272, 1905 (1996).
22. 尽管在这里所考虑的所有实例当中, 数据都处于一个单连通的组件上, 但是LLE仍然有机会 应用到多个处于不同维度的互不相交的若干流形上的数据上. 假设我们通过连接数据点及 其近邻得到一张图表. 所连接的组件的数量可以通过检查邻接矩阵的乘幂求得. 在数据中 不同的连接组件上的求解特征向量的问题, 本质上会减弱在LLE的作用. 因此, 他们最好被 解释为位于不同的流形上, 并且最好让LLE对其单独分析.
23. 如果近邻对应于时间维度上的附近观察, 那么重建权重可以在线计算(在数据本身进行收集 的时候), 并且嵌入向量可以通过对角化稀疏带状矩阵来得到.
24. R. A. Horn, C. R. Johnson, Matrix Analysis (Cambridge Univ. Press, Cambridge, 1990).
25. Z. Bai, J. Demmel, J. Dongarra, A. Ruhe, H. van der Vorst, Eds., Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide (Society for Industrial and Applied Mathematics, Philadelphia, PA, 2000).
26. D. D. Lee, H. S. Seung, Nature 401, 788 (1999).
27. R. Tarjan, Data Structures and Network Algorithms, CBMS 44 (Society for Industrial and Applied Mathematics, Philadelphia, PA, 1983).
28. I. T. Jolliffe, Principal Component Analysis (Springer-Verlag, New York, 1989).
29. N. Kambhatla, T. K. Leen, Neural Comput. 9, 1493 (1997).
30. 感谢 G. Hinton 和 M. Revow 二人(多伦多大学)分享了他们在分割与姿态估计上的未公开的 工作, 这促使我们去”思考全局, 适应局部”. 感谢 J. Tenenbaum (斯坦福大学)分享了 他的Isomap算法的代码和许多关于他的工作上的促进性的讨论. 感谢 D. D. Lee (贝尔实验室) 和 B. Frey (滑铁卢大学)之前所做的关于单词数据与人脸图像数据的工作. 感谢 C. Brody, A. Buja, P. Dayan, Z. Ghahramani, G. Hinton, T. Jaakkola, D. Lee, F. Pereira, 和 M. Sahani 所提的有帮助的建议. 再次感谢盖茨比慈善基金会, 美国国家科学基金会, 美国国家科学院和加拿大工程研究理事会的支持

7 August 2000; accepted 17 November 2000