[渣翻] Laplacian Eigenmaps and Spectral Technique for Embedding and Clustering

嵌入与聚类中的拉普拉斯特征映射和谱方法

原文链接 [click]

Abstract

借鉴拉普拉斯图与作用在流形上的拉普拉斯算子之间的一致性, 以及与热方程之间的联系, 我们提出了一个几何动机算法, 用于构造表示用于从嵌入在高维空间中的低维流形的所采样的数据. 该算法提供了近似于局部保持性非线性降维的计算效率, 并且与聚类有着自然联系. 同时考虑了一些应用.

Main Body

在人工智能, 信息检索和数据挖掘到的很多领域, 我们经常会面对本质上低维的数据分布一个非常高维的空间中. 例如, 对一个固定的物体用一个移动的照相机进行取样所获得的$n \times n$的灰度图像, 产生了在$R^{n^2}$的数据点. 然而, 同一个物体的所有照片的空间的本质上的维度是摄像机的自由度的个数, 实际上这个空间是一个自然地嵌入在$R^{n^2}$的一个流形结构. 尽管大体上有很多方法用于降维, 但是最流行的方法并不会明显地去斟酌数据有可能从属的流形结构. 最近, 这类低维数据的表示问题得到了一定的关注. 在这篇论文当中, 我们展示了一个新的算法和相关的几何动机降维的分析框架.

算法的核心非常简单, 具有较小的局部计算量和稀疏特征值问题. 问题的解反映出流形的本质上的几何结构. 在确定最理想的嵌入的过程中所使用的拉普拉斯算子保证了解的正确性. 从数据点所获取的拉普拉斯矩阵可以看作一个确定在流形上的拉普拉斯算子. 数据的嵌入映射可从确定在整个流形上的自然映射得到. 此处的分析框架使得两者联系更为明显. 尽管这种联系对于几何学家和图谱理论的专家而言很熟悉, 但是直到现在依然没有数据表示上的任何应用. 而通过热核与拉普拉斯矩阵之间的联系使得我们有能力有准则地去选取图的权重.

拉普拉斯特征选取算法的局部保留特性使得数据在相当程度上不必受噪音和错误点的影响. 而这个的副产物就是该算法暗中强调了在数据上的自然聚类. 谱聚类算法在学习领域与计算视觉领域的联系变得更为明显. 根据Roweis和Saul(2000), 以及Tenenbaum et al(2000), 我们注意到生物上的感知装置在面对高维刺激时必须还原成低维的结构. 可能有人会说, 如果通过该方法发现的这种低维结构本质上是局部的, 那么便可以自然地进行聚类, 同时可以作为类生物感知发展的基础.

The Algorithm

在${R}^l$中的$k$个点$x_1, \cdots, x_k$上, 我们建立一个由$k$个节点的赋权图, 其中, 每个数据点即为图中节点, 图的边集为所有节点与其近邻连接所成边的集合.

1. 第一步: [建图] 对于两点$i, j$, 当$x_i, x_j$“距离近”的时候, 连接两点. 这里有两种方法:

   (a) $\epsilon$-球. [参数 $\epsilon \in {R}$] 当$x_i, x_j$满足$\|x_i - x_j\|^2 < \epsilon$时, 连接两点.

   优势: 基于几何方面考虑, 天然的满足对称性.

   劣势: 经常趋向于将图变成多个连通块, 同时很难确定参数 $\epsilon$

   (b) $n$ 近邻. [参数 $n \in {N}$] 当节点$i, j$满足节点$i$是节点$j$的$n$近邻, 或节点$j$是节点$i$的$n$近邻时, 连接两点.

   优势: 选择简单, 趋向于构建连通图.

   劣势: 缺乏几何直观性.

2. 第二步: [选择权重] 同样我们有两种方法用来确定边的权重:

   (a) 热核. [参数 $r \in {R}$] 如果节点$i, j$相连, 则设置其权重为

   $$W_{ij} = \exp\{-\frac{ \|x_i - x_j\|^2 }{t}\}$$

   这种选择权重的理由将在稍后提供.

   (b) 直观法. [没有参数] 当且仅当节点$i, j$相连时, 设置其权重$W_{ij} = 1$. 即避免了选择参数$t$的必要性的简化.

3. 第三步: [特征映射] 假设之前构建的图$G$是一个连通图, 否则的话就对图中每一个连通块进行这一步的处理.

   计算一般化的特征值问题的特征值与特征向量:

   $$L y = \lambda D y$$

   其中, 权值矩阵$D$是以矩阵$W$的各行(或列, 因为$W$为对称矩阵)元素之和为对角元素的对角矩阵. 即$D_{ii} = \sum_j W_{ji}$. 令$L = D - W$, $L$为拉普拉斯矩阵. 拉普拉斯矩阵是一个对称正定矩阵, 可以认为是一个对用在图$G$的节点集的一个算子.

   不妨令$y_0, \cdots, y_{k-1}$为式(1)的解, 并且根据其对应的特征值按从小到大排列, 即$y_0$对应着最小的特征值(实际上为0). 则原始数据$x_i$在低维空间$R^m$的嵌入结果可以由$( y_1(i), \cdots, y_m(i))$得到.

Justification

回忆之前给出的利用数据集通过连接数据点与其近邻点所构造出的赋权图$G(V,E)$. 考虑将联通赋权图$G$映射到一条直线, 使得相连的点能够尽可能的保持相邻的问题. 我们希望选择一组$y_i \in R$, 在合适的条件约束下最小化函数

$$\sum_{i, j}{ (y_i - y_j)^2 W_{ij} }\qquad\text{(1)}$$

令$y = (y_1, y_2, \cdots, y_n)^T$ 为图映射到直线上的结果. 首先注意到对于任意的$y$, 满足方程

$$\frac 12 \sum_{i, j}{ (y_i - y_j)^2 W_{ij} } = y^T L y\qquad\text{(2)}$$

和之前相同, $L = D - W$. 观察该方程, 注意到$W_{ij}$是对称的, 并且$D_{ii} = \sum_j W_{ji}$. 因此, $\sum_{i, j}{ (y_i - y_j)^2 W_{ij} }$可以展开写成

$$\sum_{i, j}{ y_i^2 + y_j^2 - 2y_iy_j) W_{ij} } = \sum_{i}{ y_i^2 D_{ii} } +\sum_{j}{ y_j^2 D_{jj} } -2 \sum_{i, j}{ y_iy_j W_{ij} }= 2 y^T L y$$

因此, 这个最小值问题可以化简为寻找$arg\min_{ y^T D y = 1} { y^T L y}$.

其中约束$y^T D y = 1$移除了在嵌入过程中的任意缩放因子. 矩阵$D$提供了图中节点的一个天然的度量. 从式(2)当中, 我们可以看出矩阵$L$是一个半正定矩阵, 并且向量$y$使得目标函数最小化, 通过计算一般的特征值问题$L y = \lambda D y$.

令$1$是一个所有元素取值为$1$的常量函数. 很显然可以得出, $1$是一个特征值为$0$的特征向量. 而当这个图是连通图时, $1$是特征值$\lambda = 0$的唯一的特征向量. 为了消除这种使得整张图的节点折叠到实数$1$的这种平凡解, 我们添加额外的正交约束条件, 去得到

$$y_{opt} = arg\min_{\substack{y^T D y = 1 \\y^T D 1 = 0}} { y^T L y}$$

这样, 解$y_{opt}$现在是通过最小非零特征值所对应的特征向量而得到. 更普遍地讲, 图$G$到$R^m(m > 1)$空间的嵌入结果可以通过$n \times m$的矩阵$Y = [ y_1\ y_2\ \cdots y_m]$来求得. 其中, 矩阵$Y$的第$i$行, 设其为$Y_i^T$, 提供了第$i$个节点的嵌入坐标. 因而我们需要最小化函数

$$\sum_{i, j}{ (Y_i - Y_j)^2 W_{ij} } = {tr}(Y^TLY)$$

即求解

$$Y_{opt} = arg\min_{Y^T D Y = I} {{tr} (Y^TLY)}$$

对于一维嵌入问题, 这样的约束可以防止数据折叠到一个点上. 而对于$m$维的嵌入问题,这样的约束可以防止类似的情况, 即防止数据折叠到一个小于$m$维的子空间当中.

The Laplace-Beltrami Operator

考虑$m$维的嵌入在$R^k$的光滑流形$M$. 其黎曼结构(度量张量)由在$R^k$的标准黎曼结构导出. 假设存在映射$f: M \to R$. 其梯度函数$\nabla f(x)$(局部坐标下可以写做$\nabla f(x) = \sum_{i=1}^n{\frac{\partial f}{\partial x_i}\partial_{x_i}}$)是一个在流形上的向量场, 满足对于充分小的$\delta x$(在局部坐标图中)

$$|f(x + \delta x) - f(x)| \approx|\langle\nabla f(x), \delta x \rangle| \le\|\nabla f\| \|\delta x\|$$

因此, 我们注意到当$\|\nabla f\|$很小时, $x$附近的点将被对应到靠近$f(x)$的点上. 因此我们试图寻找一个映射关系$f$, 使得其具有最佳平均局部保持性

$$arg\min_{\|f\|_{L^2( M) = 1}}{\int_{ M}{\| \nabla f(x) \|^2}}$$

最小化$\int_{ M}{\| \nabla f(x) \|^2}$直接对应于在图上最小化$Lf = \frac 12 \sum_{i, j}(f_i - f_j)^2W_{ij}$. 最小化平方梯度简化了寻找拉普拉斯算子$L$的特征函数的过程. 注意到$L \triangleq {div} \nabla(f)$, 其中${div}$表示散度. 它满足斯托克斯定理, 即${div}$和$\nabla$是两个正式的伴随算子. 例如对于函数$f$与向量场$X$, 则有$\int_{ M}\langle X, \nabla f\rangle = \int_{ M}{div}(X) f$. 因此

$$\int_{ M}\| \nabla f \|^2 = \int_{ M}{L}(f)f f$$

注意到${L}$是半正定的, 并且使得函数$\int_{ M}\| \nabla f \|^2$最小的$f$必然是${L}$的一个特征函数.

Heat Kernels and the Choice of Weight Matrix

定义在流形$M$上的可微函数的拉普拉斯算子是与热量流动密切相关的. 令 $f: M \to R$是初始状态的热分布函数, $u(x, t)$是在$t$时刻的热分布函数($u(x, 0) = f(x)$). 热传递方程是一个偏微分方程, $\frac{\partial u}{\partial t} = {L} u$. 方程的解的形式为$u(x, t) = \int_{ M}H_t(x, y)f(y)$, 其中$H_t$是热核函数, 即该偏微分方程的格林函数. 所以有

$$L f(x) = L u(x, 0) = \left( \frac{\partial}{\partial t}[\int_{ M}H_t(x, y)f(y)] \right)$$

局部性地, 热核函数与高斯函数几乎相同, 即$H_t(x, y) \approx (4\pi t)^{-n/2} \exp\{ -\frac{ \|x - y\|^2 }{4t} \}$, 其中$\|x - y\|$($x$和$y$在同一个局部坐标系下)与$t$同样足够小, 并且$n = {dim} M$. 注意到当$t$趋向于$0$的时候, 热核函数$H_t(x, y)$变得局部快速增长, 并且趋向于狄拉克的$\delta$-函数, 即$\lim_{t \to 0}\int_{ M}H_t(x, y)f(y) = f(x)$. 因此, 对于充分小的$t$, 根据求导的定义, 可得到

$$L f( x_i) \approx-\frac 1t[f(x) -(4\pi t)^{-\frac n2}\int_{ M}\exp\{ -\frac{ \|x - y\|^2 }{4t} \} f(y) d y ]$$

如果$x_1, \cdots, x_k$是流形$M$上的数据点, 那么等式可以进一步化简为

$$L f( x_i) \approx-\frac 1t[f( x_i) -\frac 1k (4\pi t)^{-\frac n2}\sum_{x_j:0<\|x_j - x_i\|<\epsilon}\exp\{ -\frac{ \|x_i - x_j\|^2 }{4t} \} f(x_j) ]$$

系数$1/t$是全局性的, 并不会影响到离散拉普拉斯矩阵的特征向量. 既然可能不知道流形$M$的潜在维度, 我们设置$\alpha = \frac 1k (4\pi t)^{n / 2}$. 注意到常数函数的拉普拉斯矩阵为零, 我们可以很快的得到$\alpha ^{-1} = \sum\limits_{x_j:0<\|x_j - x_i\|<\epsilon}{\exp\{ -\frac{ \|x_i - x_j\|^2 }{4t} \}}$. 然而注意到无需考虑$\alpha$, 因为图的拉普拉斯矩阵$L$会帮选择出正确的乘数. 最后, 我们可以推导出选取确定图中边权给邻接矩阵$W$的方法

$$W_{ij} = \begin{cases}\exp\{-\frac{ \|x_i - x_j\|^2 }{4t}\}, & \text{if } \|x_j - x_i\|<\epsilon; \\0, & \text{otherwise}\end{cases}$$

Example

例1 玩具图像例子

考虑随机地在$40 \times 40$的区域中有水平条或垂直条的二进制图像. 我们选择了1000个这样的图像, 每一个图像随机包含一个水平条, 或者一个垂直条(共有500个含有水平条的图像和500个含有垂直条的图像). 图1展示了应用拉普拉斯映射的结果以及与PCA方法的结果比较.

例2 布朗语料库的单词例子

图2展示了选用了布朗语料库(提供约百万个单词的电子格式)中频率前300的单词的一项实验. 每个单词被表示为考虑到其左邻与右邻的一个$600$维的一个向量(通过语料库的两个单词的词组的统计进行计算).

例3 演讲例子

在图3, 我们认为应用拉普拉斯特征匹配算法到讲话的一句话的频率为1KHz的采样数据后, 可以得到数据的低维表示. 在5毫秒内可以计算出每30毫秒的语音限号块的短时傅里叶频谱, 产生685个包含256个傅里叶系数的向量. 每一个向量根据其自身所属的语音段进行标记. 图4在二维坐标系展示了数据点的拉普拉斯表示. 这两个”辐条”主要分别对应于摩擦音与发音终止. 中央部分主要对应于像元音, 鼻音, 和半元音等周期性声音. 图5展示出了空间的三个不同区域.

Figures

图 1

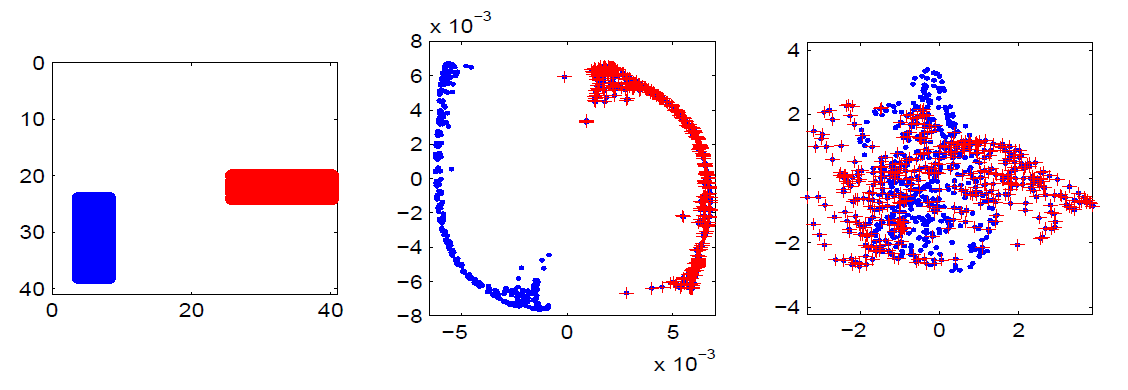左边的子图展示了一个水平条和一个垂直条. 中间的子图是将所有图像数据用拉普拉斯特征匹配后的在二维空间的表示. 右边的子图展示了通过使用主成分分析法所选取的前两个主要分量的数据表示. 图中用”.”表示垂直条, 用”+”表示水平条.

图 2

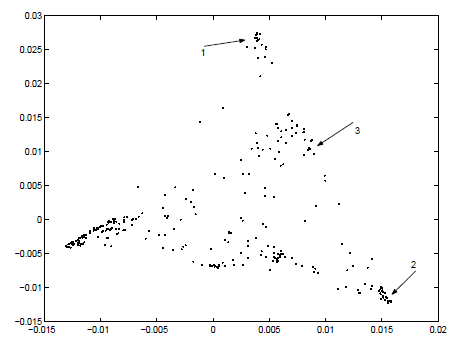布朗语料库中300个最频繁的单词的频域谱表示.

图 3

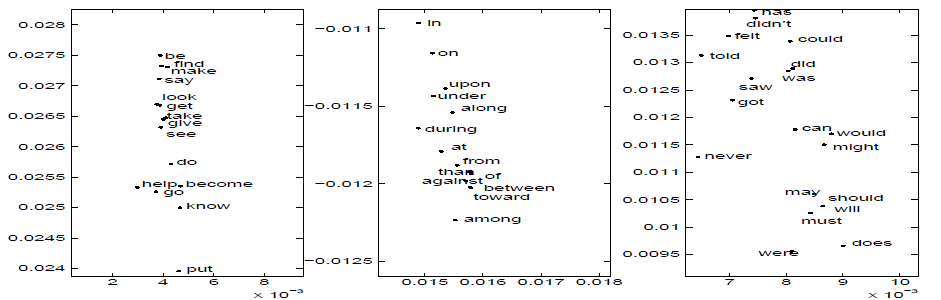三个子图从左到右展示的是图2中用箭头标注的片段. 第一个包含动词不定式, 第二个包含介词, 第三个大多是情态动词和助动词. 我们可以观察到句法结构得到了很好的保留.

图 4

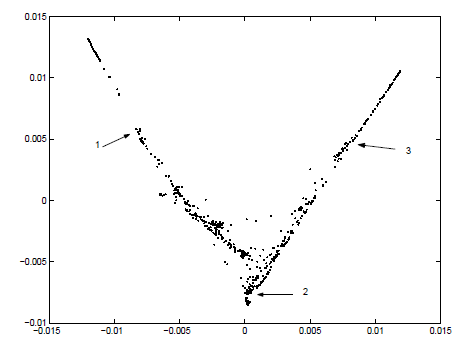685个讲话数据点的二维拉普拉斯频域谱表示.

图 5

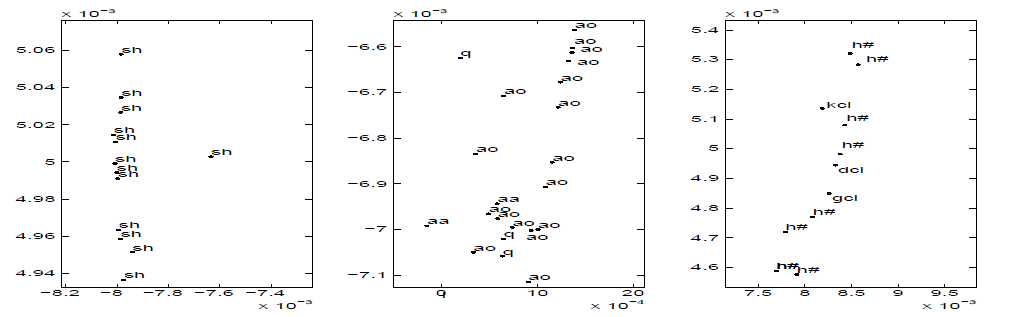上图从左到右展示了图4中的三个选中的区域. 注意到所选择区域的语音是相似的. 注意, 用相同的符号标注的数据点, 在发声过程中, 可能在不同点得到的同音素的现象. 符号”sh”表示单词”she”的摩擦音, “aa”, “ao”分别表示单词”dark”, “all”. “kcl”, “dcl”, “gcl”表示分别遇到词尾”k”, “d”, “g”时发音终止. “h#”表示没有发声.

References

[1] Fan R. K. Chung, Spectral Graph Theory. Regional Conference Series in Mathematics, number 92, 1997

[2] Fan R. K. Chung, A. Grigor’yan, S. T. Yau, Higher eigenvalues and isoperimetric inequalities on Riemannian manifolds and graphs. Communications on Analysis and Geometry, to appear

[3] S. Rosenberg, The Laplacian on a Riemmannian Manifold. Cambridge University Press, 1997

[4] Sam T. Roweis, Lawrence K. Saul, Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science, Vol 290, 22 Dec.2000

[5] Jianbo Shi, Jitendra Malik, Normalized Cuts and Image Segmentation. IEEE Transactions on PAMI, vol 22, no 8, August 2000

[6] J. B. Tenenbaum, V. de Silva, J. C. Langford, A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science, Vol 290, 22 Dec.2000